Un dimanche par mois de 17h à 19h à la salle des 4 Chemins (41 rue Lécuyer 93300 Aubervilliers)
Un dimanche par mois de 17h à 19h à la salle des 4 Chemins (41 rue Lécuyer 93300 Aubervilliers)
3 octobre 2021
→ argumentaire
→ vidéo du cours
→ texte de la leçon
21 novembre 2021
→ argumentaire
→ vidéo du cours
→ texte de la leçon
5 décembre 2021
→ argumentaire
→ vidéo du cours
→ texte de la leçon
9 janvier 2022
→ argumentaire
→ vidéo du cours
→ texte de la leçon
6 février 2022
→ argumentaire
→ vidéo du cours
→ texte de la leçon
20 mars 2022
→ argumentaire
→ vidéo du cours
→ texte de la leçon
3 avril 2022
→ argumentaire
→ vidéo du cours
→ texte de la leçon
22 mai 2022
→ argumentaire
→ vidéo du cours
→ texte de la leçon

Nos temps contemporains, profondément désorientés par l’échec des émancipations politiques à la fin du XX° siècle, désespèrent de l’humanité et s’enfoncent dans une méfiance généralisée, exaspérée par une conception naturalisante de l’animal humain qui prêche la résignation servile à une inéluctable finitude et subordonne toute activité à une gestion citoyenne des déchets sous horizon de mort.
Pour rétablir les conditions intellectuelles d’une confiance rationnelle en l’humanité, il nous faut les mathématiques modernes !
Prenons exemple sur Lautréamont (1869) : « Ô mathématiques sévères, merci pour les services innombrables que vous nous avez rendus. Merci pour les qualités dont vous avez enrichi notre intelligence. Sans vous, nous aurions peut-être été vaincus. Vous nous donnâtes la froideur, la prudence opiniâtre, la logique. Avec vos syllogismes, notre intelligence sentit s’accroître ses forces audacieuses. »
Si la pensée mathématique ne saurait nous livrer sur un plateau une conception émancipée de l’humanité et de l’infinité dont elle est capable – c’est l’affaire de la pensée politique de mettre en œuvre les idées que l’humanité soutient contradictoirement d’elle-même -, les mathématiques sont essentielles pour formaliser les conditions intellectuelles de possibilité d’une telle émancipation. Et si liberté nomme bien la capacité de transformer une contingence rencontrée en la discipline subjective d’une nécessité existentielle, alors Georg Cantor pouvait légitimement affirmer que « l’essence des mathématiques est leur liberté ».
Prenons donc appui sur leur libre subjectivité, sur leur persévérance face aux adversités et impasses (« C’est un principe cardinal en mathématiques de ne pas rejeter une bonne idée simplement parce qu’elle ne marche pas. » Ian Stewart), sur leur capacité de travailler collectivement à long terme, en partage égalitaire des intelligences, dans la confiance en leur propre puissance – les théories mathématiques avancent à échelle de plusieurs siècles, non de quelques décennies, moins encore d’une simple existence individuelle.
Pour cela, comprenons comment s’est constituée la modernité mathématique avant Cantor (de 1828 jusqu’en 1858, via 1848 et donc parallèlement à la modernité politique post-Révolution française), en étudiant six théories mathématiques couvrant les principaux continents de la mathématique (arithmétique, géométrie, algèbre, analyse et topologie) et susceptibles, chacune à sa manière, d’éclairer ce que pensée moderne veut intellectuellement dire.
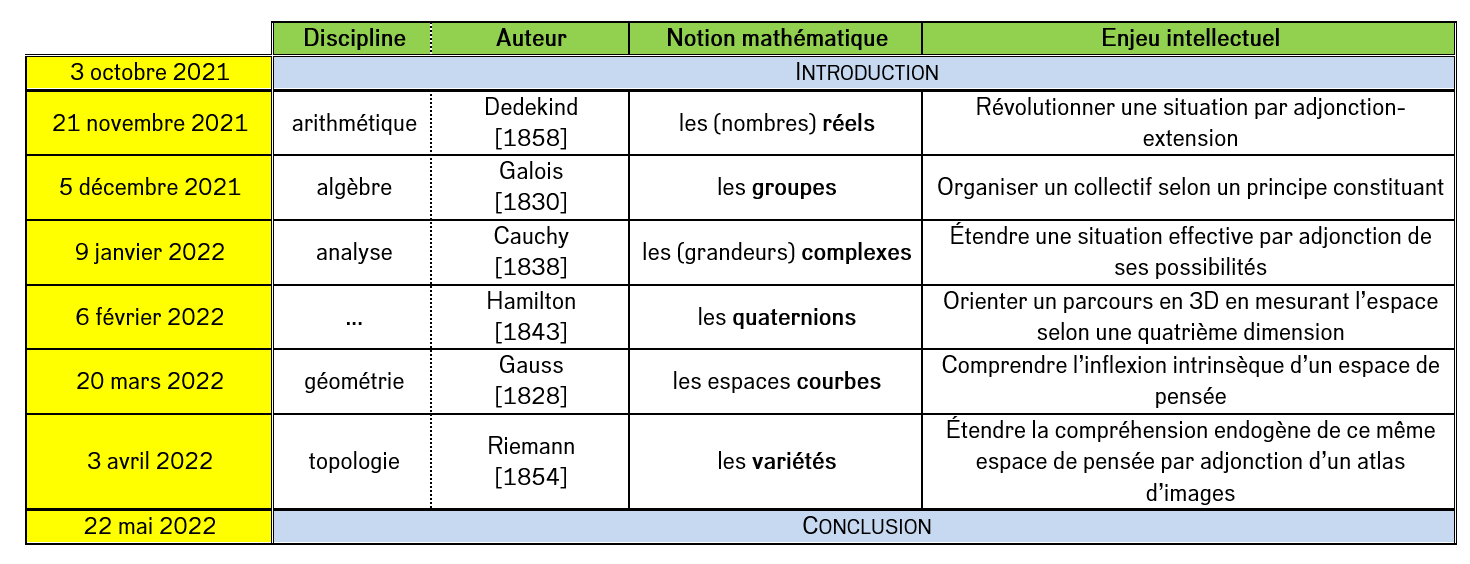
Nous retiendrons pour cela six théories :
1) la théorie arithmétique des nombres réels (Dedekind, 1858), pour éclairer ce que révolutionner par adjonction-extension veut dire ;
2) la théorie algébrique des groupes (Galois, 1830), pour éclairer ce que s’organiser veut dire et implique comme discipline des formes ;
3) la théorie analytique des grandeurs complexes (Cauchy, 1838), pour éclairer ce que étendre une situation effective (par adjonction de ses possibles) veut dire, et par là ce qu’action restreinte (entendue comme action régionale, globalement prolongeable) veut dire ;
4) la théorie des quaternions (Hamilton, 1843), pour éclairer comment s’orienter veut dire intriquer trois opérations : se repérer ⨂ se situer ⨂ se diriger ;
5) la théorie géométrique des surfaces courbes (Gauss, 1828), pour éclairer ce que propriété intrinsèque d’un espace de pensée veut dire et par là comment marcher droit dans un espace courbe ;
6) la théorie topologique des variétés (Riemann, 1854), pour éclairer ce que consistance autonome ; ce faisant, on ouvrira à la modernité mathématique post-Cantor en abordant la théorie des tenseurs (Levi-Civita, 1900) qui éclaire ce qu’intriquer causes internes et causes externes veut dire.